유효 숫자 (significant figure)
---------------------------------------------------
▶ 참고: 제1장 물질과 측정. 목차
[ https://ywpop.tistory.com/15181 ]
---------------------------------------------------
측정 장치/기구로 측정한 모든 “측정값의 마지막 숫자”는
항상 약간의 ‘불확실성’을 가지고 있습니다.
( 측정값에는 항상 기기오차와 인간(측정자)오차가 포함되어 있기 때문 )
불확실한 마지막 숫자까지 포함한
측정값의 모든 자릿수(= 숫자)를 ‘유효 숫자’라 합니다.
예) 2.5 g으로 표시한 질량의 유효 숫자는 2개, 2.5041 g은 5개.
[예제] 자의 단위는 mm이다. 이 자로 측정한 신용카드의 가로 길이는 몇 mm인가?

[해설] 자의 눈금 단위가 1 mm이므로, 1의 자리 수(까지)는 정확한 숫자이다.
만약 신용카드의 가로 길이를 85.4 mm로 읽었다면,
0.1의 자리 수는, 눈대중으로 짐작한 숫자이므로,
오차가 포함되어있는 불확실한 숫자이다.
유효숫자는 불확실한 숫자까지 포함하므로,
측정값 85.4 mm의 유효숫자 개수는 3개이다.
[참고] 위 신용카드의 가로 길이를
가령, 85.39 mm 또는 85.41 mm와 같이 읽을 수는 없다.
눈대중으로 짐작할 수 있는 숫자의 자릿수는
정확한 자릿수의 딱 한 자릿수 아래까지만 가능하다.
▶ 유효숫자의 정의
> 확실한 측정값의 자릿수에 추정(= 눈대중) 자릿수 하나를 더해서 표기한 값
> 확실한 측정값의 자릿수 = 85, 즉 1의 자릿수.
> 추정 자릿수 = 0.4, 즉 0.1의 자릿수.
( 다시 한 번 더 강조하지만, 측정값이란 실험하는 사람(인간)이
자 또는 저울 등과 같은 측정 기구(도구)를 사용해서 직접 측정한 값을 말합니다.
자신의 실험에서 자신 스스로가 직접 측정한 값. )
[ 관련 예제 https://ywpop.tistory.com/24597 ]
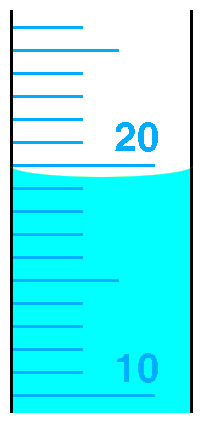
어떤 액체가 눈금 실린더에 담겨 있다.
유효 숫자를 고려하여 액체의 부피를 mL 단위로 쓰시오.
---------------------------------------------------
[측정값의 유효 숫자 개수 구하기]
▶ 0을 제외한 모든 숫자는 유효 숫자이다.
( 참고: 0의 유효숫자 개수 https://ywpop.tistory.com/24675 )
▶ 단, 유효 숫자 사이에 있는 0은 유효 숫자이다.
예) 100.2의 유효숫자 ---> 4개
예) 2.001의 유효숫자 ---> 4개
▶ 소수점을 가진 수에서 맨 앞에 있는 0은
( 소수점을 가진 수에서 유효 숫자 왼쪽에 있는 0 )
유효 숫자가 아니다, 단지 소수점의 위치를 나타내기 위해 써놓은 것일뿐.
▶ 자연수에서 유효 숫자 오른쪽에 있는 0도
유효 숫자가 아니다, 단지 자리 수를 나타내기 위해 써놓은 것일뿐.
( 참고: “유효숫자인지 아닌지 알 수 없다.”는 의견도 있습니다. )
( 참고 https://www.youtube.com/watch?v=LVe9nQo-VkU&feature=youtu.be&t=450 )
[ 관련 글 https://ywpop.tistory.com/10839 ] 자연수에서 유효숫자 오른쪽에 있는 0
(1) 0이 아닌 모든 숫자는 유효숫자이다.
단, 유효숫자와 유효숫자 사이에 있는 0은 유효숫자이다.
(2) 소수점을 가진 수에서,
유효숫자 뒤에(다음에) 나오는 0은 유효숫자이다.
(3) 자연수에서,
유효숫자 뒤에(다음에) 나오는 0은 유효숫자가 아니다,
또는 유효숫자인지 아닌지 알 수 없다.
| 측정값 | 유효 숫자 개수 |
| 1004 kg | 4 |
| 0.0023 cm | 2 |
| 0.01200 g | 4 |
| 2.0 mL | 2 |
| 1.05×10^2 g | 3 |
| 1.050×10^2 g | 4 |
| 100 m | 1 |
| 1.00×10^2 m | 3 |
| 100. m | 3 |
| 100.0 m | 4 |
예제) 다음 숫자에서 유효 숫자는 각각 몇 개인가?
a) 4867 mi
b) 56 mL
c) 60104 ton
d) 2900 g
e) 40.2 g/mL
f) 0.0000003 cm
g) 0.7 min
h) 4.6×10^19 원자
i) 0.0250×10^(-3) M
---------------------------------------------------
a) 4867 mi ---> 4개
b) 56 mL ---> 2개
c) 60104 ton ---> 5개
d) 2900 g ---> 2개
( 참고: 2900. g ---> 4개 )
e) 40.2 g/mL ---> 3개
f) 0.0000003 cm ---> 1개
g) 0.7 min ---> 1개
h) 4.6×10^19 원자 ---> 2개
i) 0.0250×10^(-3) M ---> 3개
( 지수형 숫자는 ×10^n 앞에 있는 숫자로 판단한다. )
( 예제 https://ywpop.tistory.com/6185 )
---------------------------------------------------
[완전수. Exact Numbers]
다음에 해당하는 수를 완전수라 하며,
측정값의 유효 숫자 개수를 결정할 때
완전수는 포함시키지(고려하지) 않습니다.
( 모두 실험자 스스로 측정 장치/기구를 사용하여 측정한 값이 아님 )
( 완전수의 유효숫자 개수는 무한대로 간주하므로... )
( 참고 https://ywpop.blogspot.com/2024/03/blog-post_6.html )
▶ Lange's Handbook of Chemistry와 같은 문헌에서 찾은(인용한) 값
▶ 실험 3번, 비커 3개 등과 같이 측정 장치를 사용하여 측정한 값이 아니라
세어서 구한 값 ( 예제 https://ywpop.tistory.com/4913 )
▶ 2πr(원주)에서, 2와 3.14159처럼 공식에 나와 있는 값
( 참고: 다른 의견 https://ywpop.tistory.com/11060 )
▶ 물리적/화학적 상수 값 ( 원소 주기율표에 나오는 원자량도 완전수 )
( 참고 https://ywpop.tistory.com/3255 )
▶ 단위 환산에 사용된 값 (= 환산 인자)
예) 1 in. = 2.54 cm 를 사용한 계산에서, 1과 2.54는 유효 숫자 개수와 무관하다.
( 예제 https://ywpop.tistory.com/4866 )
( 참고: 다른 의견 https://ywpop.tistory.com/11060 )
▶ 측정값들의 평균을 구하기 위해 나누어 준 값
예) 4회 측정한 값들의 평균을 구하기 위해 나누어 준 숫자 4.
( 참고 https://ywpop.tistory.com/6777 )
[유효 숫자 계산 방법]
[ https://ywpop.tistory.com/3211 ]
[ 관련 글 https://ywpop.tistory.com/11072 ] 유효숫자 처리를 하지 않는다
[ 관련 글 https://ywpop.tistory.com/13300 ] 실제 과학계산에서 유효숫자 처리(다루기)
[ 관련 글 https://ywpop.tistory.com/6868 ] 과학적 표기법
[키워드] 유효숫자 기준, 유효숫자 개념 기준, 유효숫자 정의 기준, 유효숫자의 개념 기준, 유효숫자의 정의 기준, 확정수의 정의 기준, 완전수의 정의 기준, 완전수 기준, 유효숫자 사전, 유효숫자 개념 사전, 유효숫자 정의 사전, 유효숫자의 개념 사전, 유효숫자의 정의 사전, 확정수의 정의 사전, 완전수의 정의 사전, 완전수 사전, 유효숫자 경전, 완전수 경전, 유효 사전, 유효 경전
---------------------------------------------------
[참고] 대부분 대학 교재에서 유효숫자에 대한 설명은 1장에 나옵니다.
그리고 대부분 교재에서 2, 3, 4장까지는
( 또는 시험문제라면 1학기 중간고사까지는 )
유효숫자를 고려(적용)하여 계산합니다.
그러나 여기까지가 다입니다.
이후부터는 교재마다, 교수마다 차이가 나겠지만,
유효숫자를 고려(적용)하지 않고 계산할 수도 있습니다.
0.5000 M, 2.100×10^6 J처럼
숫자 끝자리에 0을 표시하여 유효숫자를 나타낸 것 같은 분위기(?)가 아니거나,
또는 “유효숫자를 고려하여 계산하시오.”라는 요구사항이 따로 없으면,
너무 유효숫자에 연연해하지 마세요.
만약 교재에 나오는 정답이 유효숫자가 안 맞으면,
“아~ 교재 저자가 유효숫자를 고려하지 않았구나!”라고 생각하고 그냥 넘어가세요.
[ 관련 글 https://ywpop.tistory.com/13300 ] 유효숫자는 개나 줘
[유효숫자를 무시하는 경우. 유효숫자를 고려하지 않는 경우]
Q. 하버공정의 25℃에서 표준 자유 에너지 변화는 –33.3 kJ/mol이다.
ΔG값을 사용하여 25℃에서 이 반응의 평형상수 K를 구하시오.
문제 지문에 나오는 숫자는 25와 –33.3인데,
이 두 개의 숫자는 이 문제를 해결하려는 학생 또는 연구원이
직접 스스로 측정도구를 사용해서 측정한 ‘측정값’이 아니다.
케미컬 핸드북 또는 일반화학 교재 뒤쪽 부록에서 찾은
‘문헌값’이다.
“문헌값은 완전수”이므로,
평형상수 K는 유효숫자를 고려해서 답을 쓸 필요가 없다.
'화학 > 유효숫자' 카테고리의 다른 글
| 기체 상수가 포함된 유효 숫자 계산 (1) | 2015.03.27 |
|---|---|
| 유효숫자 혼합계산. (2.526/3.1) + (0.470/0.623) + (80.705/0.4326) (2) | 2015.03.25 |
| 유효숫자 계산. 4.22 K를 섭씨와 화씨로 (2) | 2015.03.21 |
| 유효숫자 계산. 1.80 * 28 + 32 (1) | 2015.03.16 |
| 유효숫자 계산(수정). 0.07×0.082×327 / (1×0.128) (0) | 2015.03.11 |
| 유효숫자 혼합 계산. 2215.7 – (4825.5 / 3.5) (1) | 2015.03.11 |
| 과학 계산에서의 유효 숫자 ★ (8) | 2015.03.09 |
| 화학 계산에서 유효 숫자(significant figure) 결정: 덧셈, 뺄셈 (3) | 2014.09.30 |
댓글