분자 오비탈 (Molecular Orbital, MO) 이론
---------------------------------------------------
▶ 참고: 제9장 분자의 기하학적 구조와 결합 이론. 목차
[ https://ywpop.tistory.com/15257 ]
---------------------------------------------------
▶ 원자 내 전자의 위치를 확률적으로 나타낸 파동 함수
⇨ 원자 오비탈 (AO, Atomic Orbital), 이듯이...
( 참고: 원자 오비탈 https://ywpop.tistory.com/7108 )
▶ 분자 내 전자의 위치를 확률적으로 나타낸 파동 함수
⇨ 분자 오비탈 (MO)
---------------------------------------------------
▶ 결합에 참여하는 AO(의 원자가전자)가 상호작용하여 새로운 MO가 만들어진다.
즉, MO는 AO의 상호작용(combination) 결과물.
AO + AO → MO
▶ Linear combination of atomic orbitals (LCAO)
원자 오비탈의 선형 결합 또는 원자 오비탈의 선형 조합
---------------------------------------------------
▶ “오비탈(orbital) = 파동 함수(wave function)의 해”
이므로, 파동의 특성을 이해할 필요가 있다.
▶ 파동(wave)의 간섭(interference)
(a) 보강 간섭: 마루와 마루의 위상이 일치 ⇨ 진폭 증가

(b) 상쇄 간섭: 마루와 골의 위상이 일치 ⇨ 진폭 = 0

---------------------------------------------------
▶ 파동 함수인 원자 오비탈, 즉 AO를 조합하여 MO를 만들 때도
2가지 방식(보강 or 상쇄)이 가능. 그 결과,
1개 AO + 1개 AO ⇨ 2개 MO 생성
(a) AO가 보강 조합되면,
⇨ 생성된 MO의 에너지 준위는 AO 보다 낮아진다. 이것을
⇨ 결합성 분자 오비탈 (bonding molecular orbital)
(b) AO가 상쇄 조합되면,
⇨ 생성된 MO의 에너지 준위는 AO 보다 높아진다. 이것을
⇨ 반결합성 분자 오비탈 (antibonding molecular orbital)
---------------------------------------------------
▶ VBT에서, “생성된 혼성 오비탈의 수 = 혼성에 참여한 AO의 수” 와 유사하게,
생성된 MO의 수 = 결합(조합)에 참여한 AO의 수
예) 수소 분자, H2의 MO
두 수소 원자의 1s 오비탈을 합치면(combination), 2개의 MO가 생성된다.
⇨ 결합성 MO(σ) 1개 + 반결합성 MO(σ*) 1개
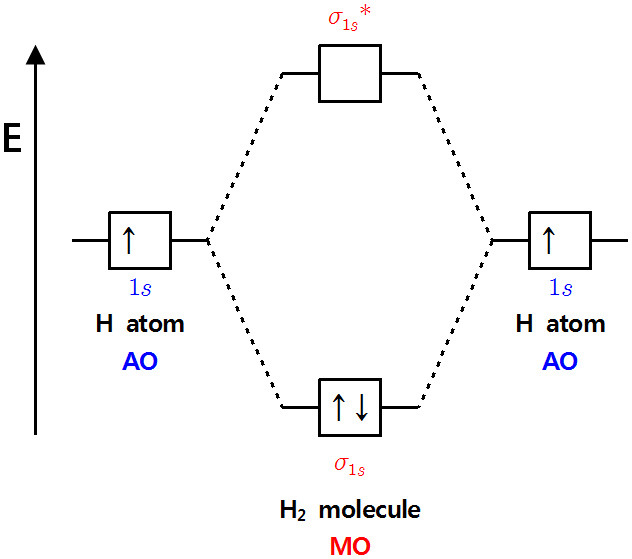
---------------------------------------------------
▶ MO의 에너지 준위
① 결합성 MO의 에너지 준위는 AO 보다 낮다 ⇨ AO 보다 안정
② 반결합성 MO의 에너지 준위는 AO 보다 높다 ⇨ AO 보다 불안정
③ 결합성 MO의 에너지 준위가 낮아진 만큼(안정해진 만큼),
반결합성 MO의 에너지 준위는 높아진다(불안정해진다).
---------------------------------------------------
▶ 결합에 참여한 두 핵 사이의 전자밀도
① 결합성 MO: 최대. 파동의 보강 간섭(a)
② 반결합성 MO: 0(영). 파동의 상쇄 간섭(b)
---------------------------------------------------
▶ MO에 전자를 채우는 규칙
기본적으로 AO와 같다.
( 참고: 원자오비탈에 전자를 채우는 방법 https://ywpop.tistory.com/2840 )
에너지가 낮은 MO부터 전자를 채운다.
up-spin(↑) 먼저, down-spin(↓) 그 다음.
① 생성된 MO의 수 = 결합에 참여한 AO의 수, 이듯이...
MO에 있는 전자 수 = AO에 있는 전자 수
② 결합성 MO에 있는 전자 수가
반결합성 MO에 있는 전자 수보다 많을수록, 안정한 분자.
[ MO Diagrams of B2, C2, N2 https://ywpop.tistory.com/5305 ]
[ MO Diagrams of O2, F2, Ne2 https://ywpop.tistory.com/3047 ]
Ne2의 MO를 보면,
“결합성 MO에 있는 전자 수 = 반결합성 MO에 있는 전자 수” 이므로,
즉 결합 차수 = 0 이므로, Ne2 이원자분자는 자연계에 존재하지 않는다.
( 참고: 결합 차수 https://ywpop.tistory.com/6879 )
[ 관련 글 https://ywpop.tistory.com/11631 ] 일산화질소(NO)의 MO
[키워드] MOT 기준문서, 분자 오비탈 이론 기준문서, 분자 오비탈 기준문서, MO 기준문서, MOT 사전, 분자 오비탈 이론 사전, 분자 오비탈 사전, MO 사전, MOT dic
'일반화학 > [09장] 분자의 기하구조와 결합 이론' 카테고리의 다른 글
| 루이스 구조식 그릴 때, 중심원자 결정방법 (0) | 2017.03.30 |
|---|---|
| 탄산의 루이스 구조 (7) | 2017.02.12 |
| NCO^- 루이스 구조 그리기 (4) | 2017.02.06 |
| CF4 루이스 구조 그리기. Lewis structure of CF4 (0) | 2016.11.24 |
| H2O는 평면 구조인가 입체 구조인가 ★ (0) | 2016.10.09 |
| 헬륨의 분자오비탈(궤도함수)과 결합차수 (0) | 2016.06.06 |
| 분자 오비탈 전자 배치, 산소 분자(O2), 이온 ★ (2) | 2016.05.30 |
| H2^+의 분자 오비탈(MO)과 결합 차수 (1) | 2016.05.27 |




댓글