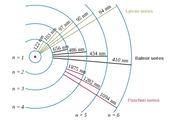
수소 원자에서 전자가 방출하는 에너지와 파장. n=1 to n=∞
- atomic hydrogen emission spectrum
수소 원자의 첫 번째 껍질로부터
전자를 완전히 제거하는데 필요한 에너지(kJ)와 파장을 계산하시오.
ΔE = R_H (1/n_i^2 – 1/n_f^2)
( 참고 https://ywpop.tistory.com/3122 )
= (2.18×10^(-18) J) (1/1^2 – 1/∞^2)
= 2.18×10^(-18) J
= 2.18×10^(-21) kJ
또는
ΔE = 13.6 eV [1/n_1^2 – 1/n_2^2]
= 13.6 [1/1^2 – 1/∞^2]
= 13.6 eV
▶ 빛의 에너지와 파장, 진동수 관계 [ https://ywpop.tistory.com/4964 ]
E = hν = h(c/λ) = hc/λ
> h = 플랑크 상수, Planck constant = 6.626 070 040×10^(-34) J•s
> ν = 빛의 진동수
> c = 빛의 속도 = 3×10^8 m/s
> λ = 빛의 파장
λ = hc / E
= [(6.626×10^(-34) J•s) (3×10^8 m/s)] / (2.18×10^(-18) J)
= 9.12×10^(-8) m
= 91.2 nm
답: 2.18×10^(-21) kJ, 91.2 nm
[참고] 1 J = 6.24151×10^18 eV 이므로,
2.18×10^(-18) J × [(6.24151×10^18 eV) / (1 J)]
= 13.6 eV
즉, 수소 원자의 이온화 에너지
= 2.18×10^(-18) J = 13.6 eV

---------------------------------------------------
수소 원자에서 전자 1개를 떼어내는데 필요한 광자의 에너지
= 수소 원자 1개에서 전자 1개를 떼어내는데 필요한 광자의 에너지
= 수소 원자 1개의 전자를 떼어내는데 필요한 광자의 에너지
---> 2.18×10^(-18) J
이 값에 아보가드로수를 곱하면,
수소 원자 1 mol의 전자를 떼어내는데 필요한 광자의 에너지
(2.18×10^(-18) J/개) × (6.022×10^23 개/mol)
= 1.31×10^6 J/mol
= 1.31×10^3 kJ/mol
[ 관련 예제 https://ywpop.blogspot.com/2023/09/calculate-ionization-energy-of-hydrogen.html ]
The removal of an electron from the hydrogen atom
corresponds to raising the electron to the Bohr orbit that has n=∞.
On the basis of this statement,
calculate the ionization energy of hydrogen in units of
(a) joules per atom and (b) kilojoules per mole.
[키워드] 수소 원자의 이온화 에너지 기준문서, 수소의 이온화 에너지 기준문서, 수소 원자 이온화 기준문서, 수소 이온화 기준문서, 무한대 기준문서, 199 방출 파장 기준문서, 199 전이 기준문서, 수소 원자의 이온화 에너지 사전, 수소의 이온화 에너지 사전, 수소 원자 이온화 사전, 수소 이온화 사전, 199 전이 사전
'일반화학 > [06장] 원자의 전자 구조' 카테고리의 다른 글
| 수소 원자의 선 스펙트럼. 4개의 선 스펙트럼 (1) | 2017.06.29 |
|---|---|
| 전자 배치의 축약. 축약형 전자 배치 ★ (0) | 2017.06.06 |
| 선 스펙트럼이 발생하는 이유 (0) | 2017.06.04 |
| 은 금속의 일함수는 436 kJ/mol (0) | 2017.05.24 |
| 하이젠베르크의 불확정성 원리 (Uncertainty Principle) (0) | 2017.05.24 |
| 빛의 에너지와 진동수, 파장 관계(예제) (2) | 2017.05.22 |
| 오비탈의 종류와 개수 (0) | 2017.05.18 |
| 파동. 파장. 진동수 ★ (0) | 2017.05.16 |

댓글