이상 기체 방정식 유도. PV=nRT
Derivation of Ideal Gas Equation. PV=nRT
[1] 보일의 법칙(Boyle's law): 부피와 압력은 반비례

[ 관련 글: 보일의 법칙 https://ywpop.tistory.com/1977 ]
[2] 샤를의 법칙(Charles's law): 부피와 온도는 비례

[ 관련 글: 샤를의 법칙 https://ywpop.tistory.com/1978 ]
[ 관련 글: 샤를의 법칙 https://ywpop.tistory.com/9578 ]
[ 관련 글: 샤를의 법칙과 절대온도(K) https://ywpop.tistory.com/3236 ]
[3] 아보가드로의 법칙(Avogadro's principle): 부피와 몰수는 비례

[ 관련 글: 아보가드로의 법칙 https://ywpop.tistory.com/1979 ]





상수 e^C 를 R 로 표기하고, 기체 상수(gas constant)라 명명하면,
( 참고: 기체상수 https://ywpop.tistory.com/49 )

P V = n R T
> P = 압력, 단위: atm
> V = 부피, 단위: L
> n = 몰수, 단위: mol
> R = 기체상수, 단위: atm•L/mol•K
( 일반적으로, 0.08206 atm•L/mol•K 사용 )
> T = 절대온도, 단위: K
n = W / M
> W = 기체의 질량, 단위: g
> M = 기체의 몰질량(= 분자량), 단위: g/mol
( 참고: n=W/M https://ywpop.tistory.com/7738 )
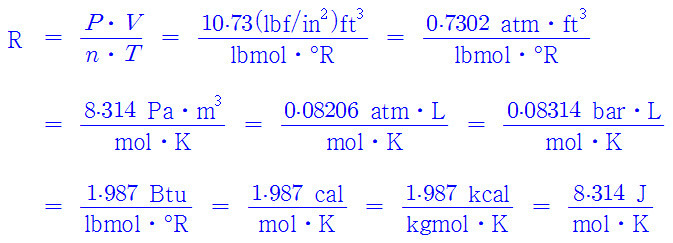

R = 0.08206 L atm mol^-1 K^-1
= 8.314 J mol^-1 K^-1
= 62.37 L torr mol^-1 K^-1
[주목] PV = nRT 식을 이용하는 계산 문제에서,
압력, 부피, 온도의 단위는
사용하는 기체상수, R의 단위와 같아야 된다.
가령, 0.08206 0.08206 atm•L / mol•K 를 사용하는데,
① 문제에서 주어진 압력이 700 mmHg 이면,
1 atm = 760 mmHg 이므로,
700 mmHg × (1 atm / 760 mmHg) = (700/760) atm
으로 환산해서 사용할 것.
② 문제에서 주어진 부피가 0.25 m3 이면,
1 m3 = 1000 L 이므로,
0.25 m3 × (1000 L / 1 m3) = 250 L
로 환산해서 사용할 것.
▶ 1 m3 = 1000 L
( 참고 https://ywpop.tistory.com/9590 )
Q) 25 L는 몇 m3인가?
A) 25 L × (1 m3 / 1000 L) = 0.025 m3
Q) 0.172 m3는 몇 L인가?
A) 0.172 m3 × (1000 L / 1 m3) = 172 L
[예제] 20℃, 750 mmHg에서 14 g의 일산화탄소(CO)가 차지하는 부피를 계산하여라.
(단, CO의 몰질량 = 28 g/mol)
V = nRT / P
= (14/28) (0.08206) (273.15+20) / (750/760)
= 12.19 L
[참고] 1 atm = 760 mmHg 이므로,
750 mmHg를 atm으로 환산하면,
750 mmHg × (1 atm / 760 mmHg)
= (750/760) atm
= 0.9868... atm
[ 관련 글 https://ywpop.blogspot.com/2024/07/15-322-ft-h2o-co2-88-lb-volume.html ]
15℃ 32.2 ft H2O CO2 88 lb volume
Calculate the volume occupied by 88 Ib of CO2 at a pressure of 32.2 ft of water and at 15℃.
15℃, 32.2 ft H2O 압력의 CO2 88 lb에 의해 점유된 부피를 계산하라.
[ 관련 글 https://ywpop.blogspot.com/2024/08/ideal-gas-equation-p-rt.html ]
ideal gas equation. P = ρRT

---------------------------------------------------
▶ 편미분(partial differential)
어떤 함수 z가 둘 이상의 변수에 의존하는 값일 때,
편미분은 어느 한 변수에 대한 의존을 나타낸다.
z가 x, y의 함수일 때, z = f(x, y)
dz는 다음과 같이 표현할 수 있다.

[키워드] PV = nRT 기준, 이상 기체 방정식 기준, 이상 기체 기준, 이상 기체 방정식 사전, 이상 기체 사전, pv nrt dic
'일반화학 > [10장] 기체' 카테고리의 다른 글
| 육플루오린화 우라늄. 60℃ 745 torr에서 UF6의 밀도 (0) | 2015.06.07 |
|---|---|
| 분압법칙과 수상포집, collection of gas over water (4) | 2015.05.30 |
| VT는 일정. 88℃ 9.6 L 수소 기체 3.4 L 온도는 (0) | 2015.05.28 |
| 켈빈온도(K)와 섭씨온도(℃). Kelvin scale and Celsius scale (6) | 2015.03.19 |
| 기체의 밀도와 몰질량 (몰분자량, 분자량) ★ (2) | 2014.10.29 |
| 기체 상수 (gas constant), R ★ (0) | 2012.10.23 |
| 기체의 양-부피 관계. 아보가드로의 법칙 (Avogadro’s law) ★ (0) | 2012.10.19 |
| 기체의 온도-부피 관계, 샤를의 법칙(Charles's law) ★ (0) | 2012.10.19 |



댓글