수소 원자에서 방출되는 빛의 에너지와 파장 계산
- atomic hydrogen emission spectrum
수소 원자에서 전자가 n=3에서 n=2로 전이될 때,
방출되는 빛의 에너지와 파장을 구하시오.
---------------------------------------------------
▶ 참고: [목차] 수소 원자가 흡수 또는 방출하는 빛의 에너지와 파장
[ https://ywpop.tistory.com/17939 ]
---------------------------------------------------
보어가 완성한 수소 원자의 n번째 궤도의 에너지 계산식

[참고] 계산식 앞에 마이너스가 붙은 이유
전자가 가장 들뜬(불안정한) 상태, 즉 전자가 너무나 들떠서
원자핵의 인력을 벗어나 이온화되는 에너지 준위를 ‘0’으로 기준 잡았기 때문이다.
0보다 안정한 상태는, 즉 0보다 작은 값은 마이너스(–)이므로,
각 오비탈의 에너지 준위는 마이너스 값을 가진다.
[ 추가 설명 https://ywpop.tistory.com/9049 ]
[ 수소 원자의 에너지 준위 그림 https://ywpop.tistory.com/7025 ]
[1] 방출되는 빛의 에너지 계산

ΔE = R_H (1/n_i^2 – 1/n_f^2)
= 2.18×10^(-18) J × (1/n_i^2 – 1/n_f^2)

[참고] 전자 1몰당 에너지 (kJ/mol) 계산
3.03×10^(-19) J은 전자 1개당 방출 에너지이므로,
전자 1 mol당 방출 에너지를 계산하면,
3.03×10^(-19) J/개 × (6.022×10^23 개/mol)
= 182466.6 J/mol = 182.47 kJ/mol
▶ 음의 부호는 방출 과정의 에너지임을 의미.
진동수 또는 파장을 계산할 땐, 절대값을 사용.
▶ 진동수 또는 파장은 항상 양수이므로,
방출 에너지로 진동수 또는 파장을 계산할때는
에너지의 절대값(양수)을 사용한다.
[2] 방출되는 빛의 파장 계산
E = hν = hc / λ
( 참고 https://ywpop.tistory.com/4964 )

[참고] 진동수를 계산하면,

답: –3.03×10^(-19) J, 656 nm
[참고]
▶ 플랑크 상수, Planck constant, h = 6.63×10^(-34) J•s
▶ 뤼드베리 상수(리드버그 상수), Rydberg constant, R_H = 2.18×10^(-18) J
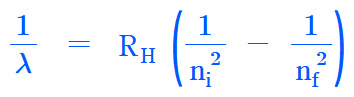
▶ 1/λ = R_H (1/n_i^2 – 1/n_f^2)
R_H, Rydberg constant = 1.097×10^5 cm^-1 or 1.097×10^7 m^-1
( 관련 예제 https://ywpop.tistory.com/11696 )
[ 관련 글 https://ywpop.tistory.com/7437 ] 수소 스펙트럼 계열. hydrogen spectral series. 수소의 방출 스펙트럼. 수소의 선 스펙트럼.
[ 관련 글 https://ywpop.tistory.com/22033 ] 처음상태 – 나중상태. 1/n_i^2 – 1/n_f^2
[ 관련 예제 https://ywpop.tistory.com/23719 ] 발머 계열의 첫 번째 선은 656.3 nm의 파장
[키워드] Rydberg 상수, 수소원자 전자전이 기준문서, 수소원자 스펙트럼 기준문서, 마이너스 이유, 보어 계산식 기준문서, 수소원자 에너지준위 기준문서, 에너지 준위 마이너스, 에너지 준위 앞에 마이너스가 붙는 이유, 에너지 준위 앞에 마이너스 이유, 32 전이 기준문서, 32 방출 파장 기준문서
---------------------------------------------------
[예제]
According to the equation for the Balmer line spectrum of hydrogen,
a value of n = 3 gives a red spectral line at 656.3 nm,
a value of n = 4 gives a green line at 486.1 nm,
and a value of n = 5 gives a blue line at 434.0 nm.
Calculate the energy (in kJ/mol) of the radiation
corresponding to each of these spectral lines.
[풀이]
E = hν = hc / λ
---> 전자 1개당 에너지
E = N_A × hc / λ
---> 전자 1 mol당 에너지
N_A × hc 를 계산하면,
(6.022×10^23 /mol) (6.626×10^(-34) J•s) (3.00×10^8 m/s) (1 kJ / 1000 J) (1 nm / 10^(-9) m)
= (6.022×10^23) (6.626×10^(-34)) (3.00×10^8) (1 / 1000) (1 / 10^(-9))
= (119705.316 kJ/mol) × nm
E = N_A × hc / λ 를 계산하면,
n = 3: [(119705.316 kJ/mol) × nm] / 656.3 nm = 182.39 kJ/mol
n = 4: 119705.316 / 486.1 = 246.26 kJ/mol
n = 5: 119705.316 / 434.0 = 275.82 kJ/mol
'일반화학 > [06장] 원자의 전자 구조' 카테고리의 다른 글
| 드브로이의 물질파 (matter wave, de Broglie wave) ★ (0) | 2015.06.08 |
|---|---|
| 수소 원자의 에너지 준위 차이와 전자 전이 파장 (0) | 2015.04.15 |
| 입자가속기 내 전자의 파장. 빛의 속도의 99% (4) | 2015.03.31 |
| 전자기파. electromagnetic wave (4) | 2015.03.12 |
| 왜 전자 껍질(오비탈)의 이름이 K L M N일까요? (1) | 2014.11.14 |
| 한 벌의 양자수. a set of quantum numbers ★ (3) | 2014.10.29 |
| 양자(quantum)와 양자 역학(quantum mechnics)에 대한 짧은 개념 (1) | 2014.10.25 |
| 오비탈의 축퇴, degenerate orbital (0) | 2014.10.24 |



댓글