굴뚝높이 60 m 대기온도 27℃ 배기가스 137℃ 통풍력 1.5배
굴뚝높이가 60 m, 대기온도 27℃, 배기가스의 평균온도가 137℃일 때,
통풍력을 1.5배 증가시키기 위해서는 배출가스의 온도는 얼마가 되어야 하는가?
(단, 굴뚝의 높이는 일정하고 배기가스와 대기의 비중량은 1.3 kg/Nm3이다.)
① 약 230℃
② 약 280℃
③ 약 320℃
④ 약 370℃
통풍력, Z (mmH2O) 계산 공식
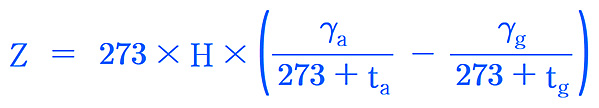
Z = 273×H×[γ_a / (273 + t_a) – γ_g / (273 + t_g)]
> H: 굴뚝높이 (m)
> γ_a: 공기의 비중량
> γ_g: 배기가스의 비중량
> t_a: 공기의 온도 (℃)
> t_g: 배기가스의 온도 (℃)
[1] 현재 통풍력
Z = 273×60×[1.3 / (273 + 27) – 1.3 / (273 + 137)]
= 19.0434 mmHg
[2] 1.5배 증가 통풍력
배출가스의 온도 = x 라 두면,
1.5×19.0434 = 273×60×[1.3 / (273 + 27) – 1.3 / (273 + x)]
(1.5×19.0434) / (273×60) = 1.3 / (273 + 27) – 1.3 / (273 + x)
1.3 / (273 + x) = 1.3 / (273 + 27) – (1.5×19.0434) / (273×60) = 0.00258943
273 + x = 1.3 / 0.00258943 = 502.0409897
x = 502.0409897 – 273 = 229.0409897
답: ① 약 230℃
[참고] 273 × 1.3 = 354.9 ≒ 355
Z = 273×H×[γ_a / (273 + t_a) – γ_g / (273 + t_g)]
= 355×H×[1 / (273 + t_a) – 1 / (273 + t_g)]
= 355×H×[1 / T_a – 1 / T_g]
( T(K) = 273 + ℃ )
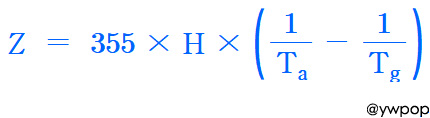
Z = 355×60×[1/300 – 1/410]
= 19.0488 mmH2O
1.5×19.0488 = 355×60×[1/300 – 1/T_g]
(1.5×19.0488) / (355×60) = [1/300 – 1/T_g]
0.0013414648 = [1/300 – 1/T_g]
1/T_g = (1/300) – 0.0013414648 = 0.0019918685
T_g = 1 / 0.0019918685 = 502.04 K
502.04 – 273 = 229.04℃
[ 관련 예제 https://ywpop.tistory.com/17277 ]
50 m의 높이가 되는 굴뚝내의 배출가스 평균온도가 300℃, 대기온도가 20℃일 때 통풍력(mmH2O)은? (단, 연소가스 및 공기의 비중을 1.3 kg/Sm3이라고 가정한다.)
Z = 355×H×(1 / T_a – 1 / T_g)
[ 관련 글 https://ywpop.tistory.com/471127 ]
비중량이 아닌 비중이 주어진 예제
19. 굴뚝 높이 100 m, 배기가스의 평균온도 200℃, 외기온도 27℃, 굴뚝내 가스의 외기에 대한 비중을 1.05라 할 때 통풍력은? 답: ④ 39.3 mmAq

[키워드] 배출가스 온도 기준, 굴뚝의 통풍력 기준, 굴뚝의 통풍력 사전
굴뚝의 높이가 60 m, 배기가스의 평균온도가 137℃일 때, 자연통풍력을 1.5배 증가시키기 위해서 배기가스온도(℃)는 얼마가 되어야 하는지 계산하시오. (단, 대기온도 27℃, 표준상태의 공기밀도는 1.3 kg/m3 기준)
'공학&기술 > 대기환경기사' 카테고리의 다른 글
| Methane Propane 용적비 1:1 혼합가스 1 Sm3 완전연소 20 Sm3 실제공기 공기비 (0) | 2024.10.28 |
|---|---|
| 연돌 배출가스 320℃ 7 m/sec 대기온도 25℃ 통풍력 65 mmH2O 연돌의 높이(m) (0) | 2024.10.02 |
| 500 m3 방안 10개비 담배 1개비당 1.4 mg 포름알데히드 (3) | 2024.07.16 |
| Sutton 확산방정식 He 40 m 최대 지표농도 1/4 (1) | 2024.04.01 |
| 1500 kg/m3 3 μm 구형입자 1 kg 입자 수 (1) | 2024.03.12 |
| 중력식 집진기에서 침강속도와 집진효율(%) (40) | 2023.09.28 |
| 굴뚝 배출가스 평균유속 피토관 동압 측정 12.8 m/s (26) | 2023.09.01 |
| 배출가스 중 SO2 2286 mg/Sm3를 ppm으로 환산 (22) | 2023.08.23 |
댓글